Tutoriel R#

Introduction#

Ceci est un notebook jupyter. C’est le support que nous allons utiliser tout au long du semestre pour les séances d’exercices. La révision des concepts présentés dans ce noteboook vous sera grandement bénéfique et vous permettra de gagner du temps lors des séances d’exercices.

Qu’est-ce que les Jupyter Notebooks et pourquoi les utiliser?.

L’environnement Jupyter Notebooks est un système hybride écrit en Python dont l’interface utilisateur s’exécute comme des applications web dans votre navigateur. Par conséquent, comme Python, les Jupyter Notebooks sont des applications open source qui facilitent la création et le partage de codes et de documents. Les carnets Jupyter fournissent un environnement dans lequel vous disposez de différents types de cellules (par exemple, celle qui est présentée ici est appelée cellule Markdown et est pratique pour la documentation, l’intégration d’images, de liens url, l’explication de ce que vous prévoyez de faire, comment, etc.) Les cellules de code sont utiles car elles peuvent être exécutées une par une et facilitent le prototypage et le débeuguage, un peu comme la division d’un scrip Matlab en sections. Ces cellules de codes peuvent être en un langage différent Python, comme R et c’est le cas de ce document. Contrairement à Matlab cependant, vous n’avez pas une vue d’ensemble de vos variables et de leurs valeurs, mais vous pouvez toujours les imprimer.

Comment utiliser les Jupyter notebooks ?#

Pour utiliser un Jupyter notebook, vous devez comprendre quelques principes de base :

Ajout et suppression de cellules

Si vous avez ouvert le notebook avec noto, vous pouvez ajouter (au-dessus ou en-dessous) et supprimer des cellules depuis le coin supérieur droit de chaque cellule.

Si vous travaillez en local avec une distribution Anaconda,vous pouvez ajouter des cellules en allant dans le menu “Insertion” et en choisissant “Ajouter au-dessus ou au-dessous” et déplacer des cellules vers le haut ou vers le bas en choisissant les flèches sous la barre à outils.

A tout moment vous pouvez changer le type de cellule : Code, Markdown,etc…

Faire tourner les cellules

Vous devrez procéder de la sorte pour exécuter le code contenu dans les cellules individuelles.

Pour exécuter une cellule individuelle, sélectionnez-la et appuyez sur “Maj+Entrée”.
Pour exécuter le notebook en entier, allez dans “Cellule->Exécuter tout”. Pour exécuter seulement les cellules au-dessus ou au-dessous, vous trouverez cela dans le même menu.
Pour éxécuter de nouveau le notebook en entier, allez dans “Kernel -> Restart and Run all” ou appuyez sur le bouton qui ressemble à un bouton d’avance rapide. Ceci efface toutes les variables stockées en mémoire et exécute le notebook depuis le début. Il est important de ré-exécuter le notebook à partir de zéro de temps en temps, par exemple lorsque vous avez atteint une étape importante pour vous assurer que vous n’avez pas de beugs. Comme le notebook stocke toutes les variables en mémoire, cela permet d’éviter les erreurs dues à la suppression d’un élément ou à l’ordre incorrect de certains éléments dans les cellules ou entre les cellules.

Bonnes pratiques

Expliquez votre raisonnement dans les cellules Markdown, de la même manière que vous le feriez dans un rapport. Vous pouvez avoir des sections, des sous-sections, écrire des paragraphes, saisir des images, etc.
Commentez votre code afin que toute personne qui ouvre votre notebook comprenne ce que vous faites.
Lorsque vous faites appel à une librairie, il est considéré comme une bonne pratique de l’importer au début du notebook.
N’oubliez pas de sauvegarder régulièrement votre notebook. Vous pouvez le faire soit avec le raccourci d’enregistrement (Ctrl+S), soit en passant par Fichier -> Enregistrer sous. Sous Fichier, vous trouverez également d’autres options telles que créer un nouveau notebook, renommer le notebook actuel, le télécharger en tant que fichier pdf, python etc…

Installation des extensions Jupyter Notebook

Les extensions Jupyter sont des modules complémentaires qui fonctionnent avec les notebooks Jupyter (et non avec Jupyter Lab) permettant d’améliorer votre productivité. Si vous êtes intéressés, vous pouvez installer quelques extensions qui sont utiles

Introduction à R#

R est un langage open source qui a été développé sur la base d’un autre langage, S, qui n’est désormais plus utilisé. R est devenu le langage privilégié de la communauté statistique. Il implémente un nombre très important de fonctions permettant de manipuler des données et de méthodes d’analyse statistiques. Il s’agit, à l’instar de Matlab ou Python, d’un langage interprété. Cela rend son utilisation typiquement plus lente qu’un langage compilé, comme C et C++, mais plus aisée puisqu’il n’est pas nécessaire de compiler une fonction pour l’utiliser. Par ailleurs, lorsque dans certaines situations, la vitesse d’exécution de R devient problématique, il est possible d’appeler depuis des routines écrites en C (nativement) ou C++ (via le package Rcpp).

Types et opérateurs#

En R, il y a différents types prédéfinis:

chaîne de caractères: string
numérique: int, float
listes: list, data.frame , tibble, etc.
booléen: bool (True or False)
facteurs: fac (niveau encodant une variable catégorielle)

Le type d’une variable est défini au moment où on lui assigne une valeur.

Exemple	Type correspondant
x = “Hello World”	string
x = 20	integer
x = 20.5	float
x = list(“apple”, “banana”, “cherry”)	list
x = c(“apple”, “banana”, “cherry”)	vector
x = True	bool

Les opérateurs sont utilisés pour faire des opérations sur des variables ou des valeurs.

Les opérateurs arithmétiques

Opérateur	Nom	Exemple
+	Addition	x + y
-	Soustraction	x - y
*	Multiplication composante par composante	x * y
/	Division	x / y
%%	Modulo (reste d’une division entière)	x %% y
^	Exponentielle	x ^ y

Les opérateurs d’affectation

Opérateur	Exemple	Comme
= ou <-	x = 5	x = 5
<-	x += 3	x = x + 3

Les opérateurs de comparaison

Opérateur	Nom	Exemple
==	Egal	x == y
!=	Différent	x != y
>	Plus grand que	x > y
<	Plus petit que	x < y
>=	Plus grand ou égal	x >= y
<=	Plus petit ou égal	x <= y

Les opérateurs logiques

Opérateur	Description	Exemple
&	Retourne Vrai si les deux déclarations sont vraies	x < 5 & x < 10
\|	Retourne Vrai si au moins une des deux déclarations est vraie	x < 5 or x < 4
!	Négation, Inverse le résultat, renvoie Faux si le résultat est vrai.	not(x < 5 and x < 10)

vecteur#

Un vecteur est un ensemble ordonné et modifiable. En R, les vecteurs se déclarent avec des avec la fonction c(). L’indexation commence à 1 en R. L’index -1 permet de supprimer le premier élément de la liste et de manière générale, les indices négatifs retirent du vecteur les éléments correspondants.

vec = c(1, pi, exp(1))
vec[1]

Voilà mon titre

On peut déclarer un vecteur d’une suite d’entiers de manière particulièrement aisée en utilisant : ou alors, avec un peu plus de possibilités, en utilisant la fonction seq

1:10 # vecteur dont les composantes sont les entiers de 1 à 10
8:-2 # vecteur dont les composantes sont les entiers de 8 à -2, dans l'ordre décroissant
seq(from = 1, to = 12, by = .25) # vecteur de 1 à 12, avec un incrément de 0.25
seq(1,12, length.out = 10) # vecteur de 1 à 12, avec un incrément constant et une longueur de 10

8
7
6
5
4
3
2
1
0
-1
-2

1
1.25
1.5
1.75
2
2.25
2.5
2.75
3
3.25
3.5
3.75
4
4.25
4.5
4.75
5
5.25
5.5
5.75
6
6.25
6.5
6.75
7
7.25
7.5
7.75
8
8.25
8.5
8.75
9
9.25
9.5
9.75
10
10.25
10.5
10.75
11
11.25
11.5
11.75
12

1
2.22222222222222
3.44444444444444
4.66666666666667
5.88888888888889
7.11111111111111
8.33333333333333
9.55555555555556
10.7777777777778
12

La fonction matrix permet de définir des matrices (en deux dimensions) en spécifiant ses éléments à l’aide d’un vecteur. Il est nécessaire de préciser le nombre de lignes et/ou de colonnes. Par défaut, la matrice se remplit par colonne mais l’option byrow = T permet de la remplir par ligne.

M = matrix(c(1,2,3,4,5,6), nc = 3)
print(M)

M[,1]  #élément à la 1ère ligne, 2ème colonne
M = matrix(c(1,2,3,4,5,6), nc = 3, byrow = T)
print(M)

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6

Pour afficher une dimension (ligne ou colonne), on laisse vide l’indice correspondant.

M[1,]  #affiche toute la 1ère ligne
M[,2]  #affiche toute la 2ème colonne

Opérations sur des vecteurs/matrices#

Voir les exemples ci-dessous:

 M %*% vec #multiplication matrice-vecteur
 M %*% matrix(vec, nc = 1) # identique; un vecteur est considere comme une matrice de taille n x 1

A matrix: 2 × 1 of type dbl
15.43803
36.01765

A matrix: 2 × 1 of type dbl
15.43803
36.01765

3 * M # est similaire a une multiplication de la matrice par un scalaire

A matrix: 2 × 3 of type dbl
3	6	9
12	15	18

3*M + 5 # est similaire a une multiplication de la matrice par un scalaire suivi d'une addition d'un scalaire

A matrix: 2 × 3 of type dbl
8	11	14
17	20	23

rep(vec, 3) # répétition de 3 fois le même vecteur  
rep(vec, each = 3) # répétition 3 fois de chaque éléments du vecteur consécutivement

1
3.14159265358979
2.71828182845905
1
3.14159265358979
2.71828182845905
1
3.14159265358979
2.71828182845905

1
1
1
3.14159265358979
3.14159265358979
3.14159265358979
2.71828182845905
2.71828182845905
2.71828182845905

Finalement, appeler un objet fait implicitement appel à la méthode print qui y est associée. Ainsi

M # affiche M
print(M[2,1]) # affiche la composante (2,1) de la matrice M 
M[2,1] # affiche aussi la composante (2,1) de la matrice M 

A matrix: 2 × 3 of type dbl
1	2	3
4	5	6

[1] 4

Les listes#

Les listes sont un type d’objets constitué d’objets. C’est particulièrement pratique pour stocker dans un même objet plusieurs informations de types différents. Il est à noter qu’un data.frame est un type particulier de liste, et donc que beaucoup de commandes sont similaires. On peut accéder aux éléments d’une liste de deux manières. En utilisant l’indice, à l’aide de deux crochets ou via leur nom, en utilisant le caractère $.

mylist <- list(x = c(2,3), y = matrix(c(1,-1,-1,2), nc = 2)) # liste de deux objets, le premier, x est un vecteur
# et le second, y, est une matrice
mylist[[1]] # on accède au premier élément
mylist$y # on accède à l'élément y
mylist$z <- T # on déclare un élément z qui est un booléen T
mylist

A matrix: 2 × 2 of type dbl
1	-1
-1	2

$x

$y

A matrix: 2 × 2 of type dbl
1	-1
-1	2

$z

TRUE

Les principales structures#

L’instruction if#

Exécutez les différents exemples ci-dessous pour vous familiariser avec sa syntaxe:

a = 33
b = 200
if(b > a) print("b is greater than a")

[1] "b is greater than a"

Si ce qui suit le if fait plus d’une ligne, l’utilisation d’accolades en guise de délimiteurs devient nécessaire.

a = 33
b = 200
if(b > a){
    print("b is greater than a")
    print(b-a)
}

[1] "b is greater than a"
[1] 167

L’indentation n’importe pas (sauf pour la lisibilité de votre code. Lorsque else est utilisé, il doit être sur la même ligne que l’accolade fermant la condition if

a = 200
b = 33
# version correcte
if (b > a)
    {
     print("b is greater than a")
} else
    {
    print("a is greater than b")
}
 
  

[1] "a is greater than b"

a = 200
b = 33
# donne une erreur
if (b > a)
    {
     print("b is greater than a")
}
else
    {
    print("a is greater than b")
}
 
  

Error in parse(text = x, srcfile = src): <text>:8:1: unexpected 'else'
7: }
8: else
   ^
Traceback:

a = 33
b = 33
# version correcte
if (b > a)
    {
     print("b is greater than a")
}else if (b == a)
    {
    print("a is equal to b")
} else
{
    print("a is greater than b")
}

[1] "a is equal to b"

Il peut y avoir un nombre quelconque de parties else if().

L’instruction while#

La boucle while permet d’exécuter un ensemble d’instructions tant qu’une condition est vraie.

i = 1
while(i < 6)
    {
  print(i)
  i = i + 1
}

[1] 1
[1] 2
[1] 3
[1] 4
[1] 5

La boucle while exige que les variables pertinentes soient prêtes. Dans cet exemple, nous avons dû définir une variable d’indexation, i, fixée à 1.

Exécutez les cellules ci-dessous pour découvrir la commande break.

i = 1
while(i < 6)
  { print(i)
  if(i == 3) break
  i  <- i + 1
   }

[1] 1
[1] 2
[1] 3

Break permet d’arrêter la boucle while même si la condition du while est toujours satisfaite.

L’instruction for#

L’instruction for que propose R est un peu différente de celle que l’on peut trouver dans d’autres langages de programmation et fonctionne davantage comme une méthode d’itération que l’on trouve dans les langages de programmation orientés objet.

Elle est utilisée pour itérer sur un vecteur ou même sur une liste (c’est-à-dire une liste, un vecteur).

De nouveau, éxécutez les différents exemples ci-dessous pour vous familiariser avec sa synthaxe:

fruits = c("apple", "banana", "cherry")
for(x in fruits)
  print(x)

[1] "apple"
[1] "banana"
[1] "cherry"

for(x in vec) #avec un vecteur
    print(x * 2)

[1] 2
[1] 6.283185
[1] 5.436564

Comme pour la boucle while, on peut utiliser break et continue pour sortir de la boucle for ou passer à l’itération suivante.

Vous avez remarqué que contrairement à une boucle for en C où l’on donne à l’utilisateur la possibilité de définir le pas d’itération et la condition de fin, l’instruction for en Python itère sur les éléments d’une séquence (qui peut être une liste, une chaîne de caractères…), dans l’ordre dans lequel ils apparaissent dans la séquence.

Exécutez les cellules suivantes pour voir l’utilité de certaines fonctions complémentaires comme seq et seq_along.

for(x in seq(2, 30, by = 3)) #commence à 2, finit à 29 et incrémente de 3
  print(x)
# seq_along permet déclare un vecteur correspondant au vecteur des indices d'un autre vecteur
seq_along(vec)
# typiquement utilisé de la manière suivante
for(i in seq_along(vec))
    vec[i]
# et qui est équivalent à 
for(i in 1:length(vec))
    vec[i]

[1] 2
[1] 5
[1] 8
[1] 11
[1] 14
[1] 17
[1] 20
[1] 23
[1] 26
[1] 29

Les fonctions#

Syntaxe des fonctions#

La syntaxe R pour la définition d’une fonction est la suivante :

myfun <- function(liste de paramètres){bloc d'instructions}

Vous pouvez choisir n’importe quel nom pour la fonction que vous créez, à l’exception des mots-clés réservés du langage, et à la condition de n’utiliser aucun caractère spécial ou accentué (le caractère souligné « _ » est permis). Une fonction peut avoir un, plusieurs ou pas de paramètres d’entrée (appelés arguments) et elle peut retourner indirectement (print) ou directement des variables (avec return). Par défaut, la dernière variable appelée dans la fonction est retournée. Exécutez les cellules ci-dessous pour vous familiariser avec les fonctions. A noter qu’en R, il n’est pas possible de retourner plusieurs objets. Toutefois il est possible de retourner une liste, qui comprend tous les objets que l’on souhaite.

compteur <- function(){ #sans paramètres d'entreé ni de sortie
    i = 0
    while(i < 3){
        print(i)
        i = i + 1
        }
} 
    
compteur()

[1] 0
[1] 1
[1] 2

compteur() #une fois définie, on peut appeler la fonction depuis une autre cellule du notebook.

[1] 0
[1] 1
[1] 2

compteur2 <- function(stop){ #avec un paramètre d'entrée
    i = 0
    while (i < stop){
        print(i)
        i = i + 1
        }
    }
compteur2(4)

[1] 0
[1] 1
[1] 2
[1] 3

On peut utiliser la syntaxe = dans un argument pour lui donner une valeur par défaut. Ainsi

compteur2 <- function(stop = 2){ #avec un paramètre d'entrée
    i = 0
    while (i < stop){
        print(i)
        i = i + 1
        }
    }
compteur2()

[1] 0
[1] 1

compteur3 <- function(stop,b = 3){ #avec 2 paramètres d'entrée, le second étant par défaut b = 3
    i = 0
    while(i < stop){
        i = i + b
        print(i)
        }
        }
print("avec deux paramètres spécifiés")
compteur3(4,2)

print("avec un seul paramètre spécifié")
compteur3(5)

[1] "avec deux paramètres spécifiés"
[1] 2
[1] 4
[1] "avec un seul paramètre spécifié"
[1] 3
[1] 6

x = compteur(4) #on peut directement attribuer ce que retourne la fonction à des variables en dehors de la fonction
print(x)

On montre comment retourner plusieurs objets via une liste.

compteur <- function(stop){ #avec un paramètre d'entrée et 2 de sortie
    i = 0
    j = 100
    while(i < stop){
        i = i + 1
        j = j - 1
        }
    return(list(i = i,j = j)) 
}
mylist <- compteur(4) # Attention à l'ordre des paramètres: x prend la valeur de i et y de j.
print(c(mylist$i,mylist$j))

[1]  4 96

myfunction <- function(x = 5){
    y = x + 2
    y # équivalent à return(y)
}
x <- myfunction(3)
print(x)

[1] 5

Portée des variables (scope)#

En R, nous pouvons déclarer des variables n’importe où dans notre script : au début du script, à l’intérieur de boucles, au sein de nos fonctions, etc. L’endroit où l’on définit une variable dans le script va déterminer l’endroit où la variable va être accessible c’est-à-dire utilisable.

Le terme de “portée des variables” sert à désigner les différents espaces dans le script dans lesquels une variable est accessible. En R, une variable peut avoir une portée locale ou une portée globale.

Les variables définies à l’intérieur d’une fonction sont appelées variables locales. Elles ne peuvent être utilisées que localement c’est-à-dire qu’à l’intérieur de la fonction qui les a définies. Tenter d’appeler une variable locale depuis l’extérieur de la fonction qui l’a définie provoquera une erreur.

example <- function(){
    loc = 5
} 
print(loc) # retourne une erreur puisque loc n'existe que dans la fonction

Error in print(loc): object 'loc' not found
Traceback:

1. print(loc)

Cela est dû au fait que chaque fois qu’une fonction est appelée, R réserve pour elle (dans la mémoire de l’ordinateur) un nouvel espace de noms (c’est-à-dire une sorte de dossier virtuel). Les contenus des variables locales sont stockés dans cet espace de noms qui est inaccessible depuis l’extérieur de la fonction.

Cet espace de noms est automatiquement détruit dès que la fonction a terminé son travail, réinitialisant les valeurs des variables à chaque nouvel appel de fonction.

Les variables définies dans l’espace global du script, c’est-à-dire en dehors de toute fonction sont appelées des variables globales. Ces variables sont accessibles (= utilisables) à travers l’ensemble du script et accessible en lecture seulement à l’intérieur des fonctions utilisées dans ce script.

Pour le dire très simplement : une fonction va pouvoir utiliser la valeur d’une variable définie globalement mais ne va pas pouvoir modifier sa valeur c’est-à-dire la redéfinir. En effet, toute variable définie dans une fonction est par définition locale ce qui fait que si on essaie de redéfinir une variable globale à l’intérieur d’une fonction on ne fera que créer une autre variable de même nom que la variable globale qu’on souhaite redéfinir mais qui sera locale et bien distincte de cette dernière.

var_globale = 5

exemple <- function(){
    var_globale = 0
    print(var_globale)
    }
exemple()        
print(var_globale)

[1] 0
[1] 5

De manière générale, il est imprudent d’utiliser une variable globale dans une fonction. En effet, il suffit que l’on redémarre une session et que l’on ne déclare pas la variable globale utilisée pour que la fonction produise une erreur difficile à repérer.

Les librairies (packages)#

Jusque là, nous avons vu les différentes structures (if, while, for) et comment implémenter une fonction. Nous allons à présent aborder ce qui fait la puissance de R grâce à sa communauté de développeurs qui créent et mettent à disposition de nombreuses librairies permettant de gagner un temps précieux.

En R, une librairie est un ensemble de fonctions, de classes d’objet et de données qui permettent de travailler sur un thème en particulier. R contient de base de très nombreuses fonctions et, contrairement à Python, il n’est pas nécessaire de charger des librairies pour effectuer la plupart des choses nécessaires dans le cadre de ce cours.

Avant toute chose, il faut les installer puis les importer sur le notebook.

Installation des packages via le notebook

La plupart des packages sont déjà préinstallés, ce qui signifie qu’il suffit de les charger. Cela se fait au moyen de la commande library. L’argument est le nom de la librairie (entre guillemet ou pas, les deux fonctionnent normalement). Par exemple, la librairie tidyverse qui regroupe de nombreuses libraires très utilisées, se charge de la manière suivante:

library("tidyverse")

Lorsque l’on souhaite utiliser une seule fonction d’une librairie, sans nécessairement charger toute la librairie, il suffit d’appeler cette fonction avec le préfixe de la librairie suivi de ::: package::function. Par exemple, si on souhaite utiliser la fonction mapvalues du package plyr qui remplace un ensemble de valeurs par autre ensemble de valeurs dans un vecteur, par exemple on remplace 1 par A, 2 par B, etc. Toutefois, cette fonction utile fait partie d’une librarie qui n’est plus en développement. Autrement dit, il est peu avisé de charger cette librarie puisque d’autres librairies ont pris le relai. Toutefois, cette fonction est relativement utile. Du coup, on souhaiterais ne faire appel qu’à elle. On procède donc comme ci-dessous.

set.seed(1) # pour fixer une graine dans le générateur de nombre aléatoire
x <- sample(1:5,size = 20, replace = T ) # On choisit de manière équiprobable et avec remise 20 valeurs entre 1 et 5,
plyr::mapvalues(x, from = 1:5, to = LETTERS[1:5]) # on remplace 1,..., 5 par A,...,E

data frames#

La manipulation de données est une opération essentielle dans R et ne nécessite donc, a priori, pas de charger une quelconque librairie. On peut donc aisément charger des fichiers .csv ou plus généralement des tables à l’aide des fonctions read.table et read.csv.
Pandas permet également d’effectuer des calculs statistiques sur tes données, par exemple avec la méthode .mean() qui permet d’obtenir la moyenne des valeurs contenues dans une colonne.

datas = data.frame(Taille = c(147 , 150 , 152 , 155 , 157 , 160 , 163 , 165 , 168 , 170 , 173 , 175 , 178 , 180 , 183), 
                                Poids = c(52 , 53 , 54 , 56 , 57 , 59 , 60 , 61 , 63 , 64 , 66 , 68 , 70 , 72 , 74))
head(datas)

A data.frame: 6 × 2
	Taille	Poids
	<dbl>	<dbl>
1	147	52
2	150	53
3	152	54
4	155	56
5	157	57
6	160	59

mean(datas$Poids) # calcule la moyenne de la colonne "Poids" 

61.9333333333333

Si par exemple, on souhaite appliquer une même fonction à toutes les colonnes d’un data.frame, on peut utiliser la fonction lapply qui prend en argument une list et qui applique une même fonction à tous les arguments. Puisqu’un data.frame est une liste, cela fonctionne comme espéré.

lapply(datas, mean)

$Taille: 165.066666666667
$Poids: 61.9333333333333

lapply(datas, median)

$Taille: 165
$Poids: 61

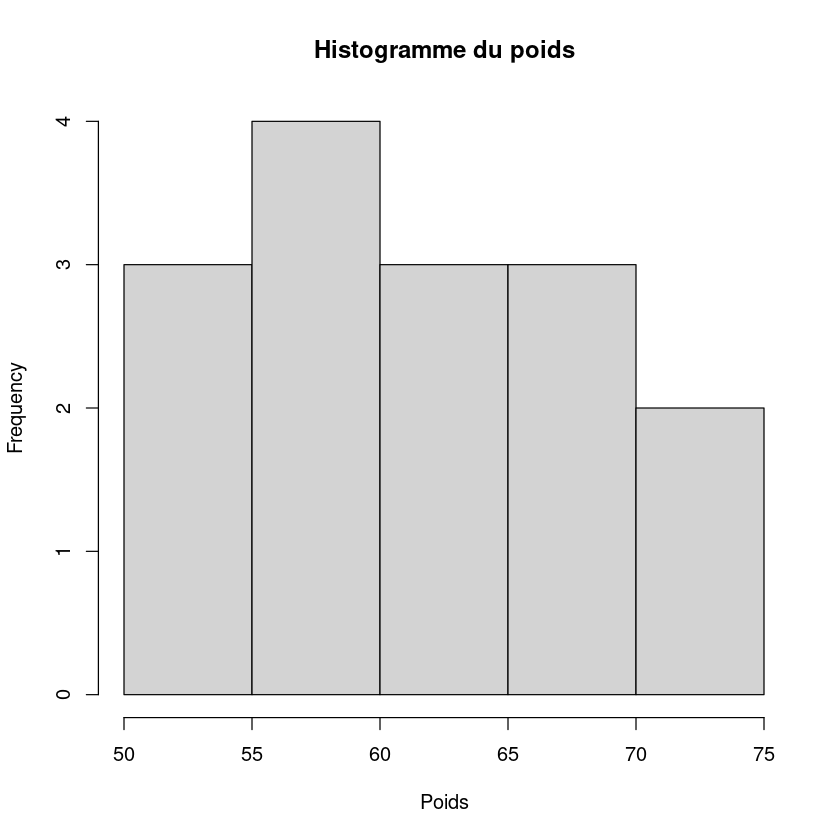
La fonction hist permet de produire facilement un histogramme. Par exemple

hist(datas$Poids, main = "Histogramme du poids", xlab = "Poids")

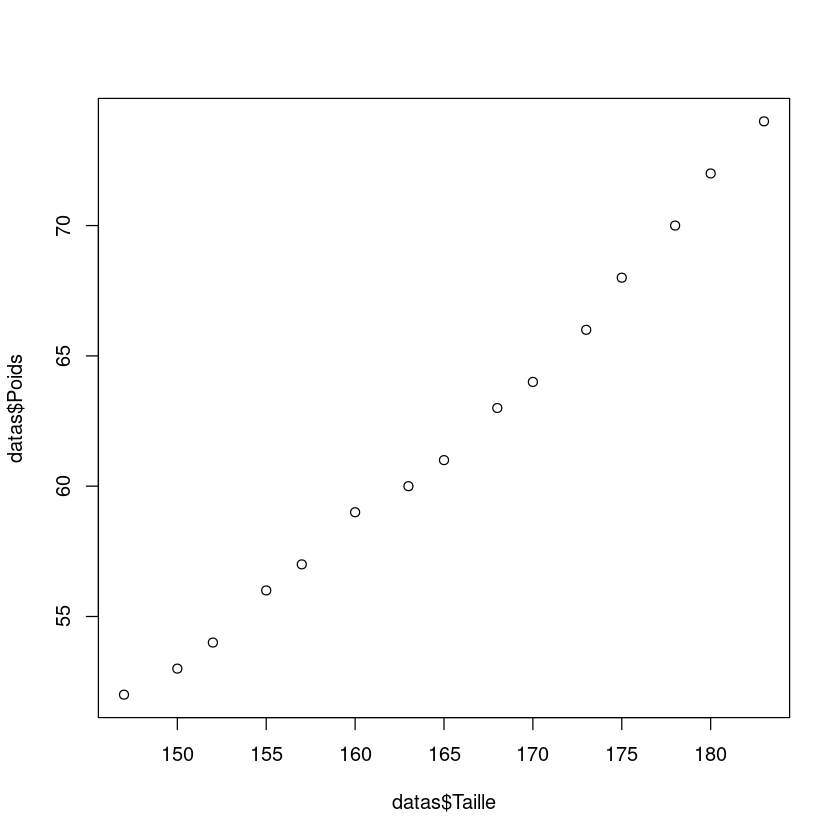
Un nuage de points s’obtient en utilisant la fonction plot

plot(x=datas$Taille, y=datas$Poids)

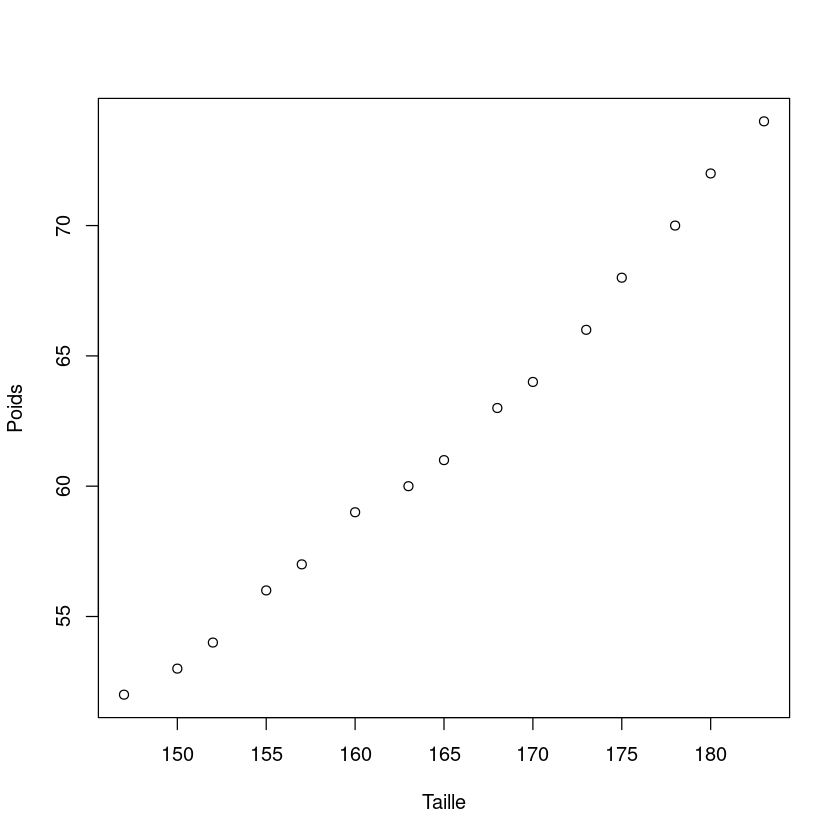
Parfois, lorsque l’on travaille avec un data.frame, il est utile de s’éviter de devoir systématiquement appeler le data.frame. Cela se fait via la fonction with.

with(datas, plot(x = Taille, y = Poids)) # with prend comme premier argument le nom de l'environnement,
# puis l'expression à évaluer

Opérations numériques#

La fonction numeric(n) renvoie un vecteur de n chiffres, tous égaux à 0.

numeric(10)

X = c(1,2,3,4,5)
mean(X)   #mean est la fonction pour calculer la moyenne d'un vecteur

M = matrix(c(1,2,3,3,5,6,7,8,9), nc = 3)
y = c(1,1,1)
det(M) # calcule le déterminant de M
x = solve(M,y) # résout l'équation Ax = y
print(x) # affiche la solution x

-6

[1] -0.1666667  0.0000000  0.1666667

dim(M) # renvoit la taille de M: matrice 3x3

rowSums(M) # permet de faire la somme sur les lignes
colSums(M) # permet de faire la somme sur les colonne

t(M) # matrice transposée de M

A matrix: 3 × 3 of type dbl
1	2	3
3	5	6
7	8	9

Plots#

R gère de manière native des graphiques performants et relativement intuitifs.

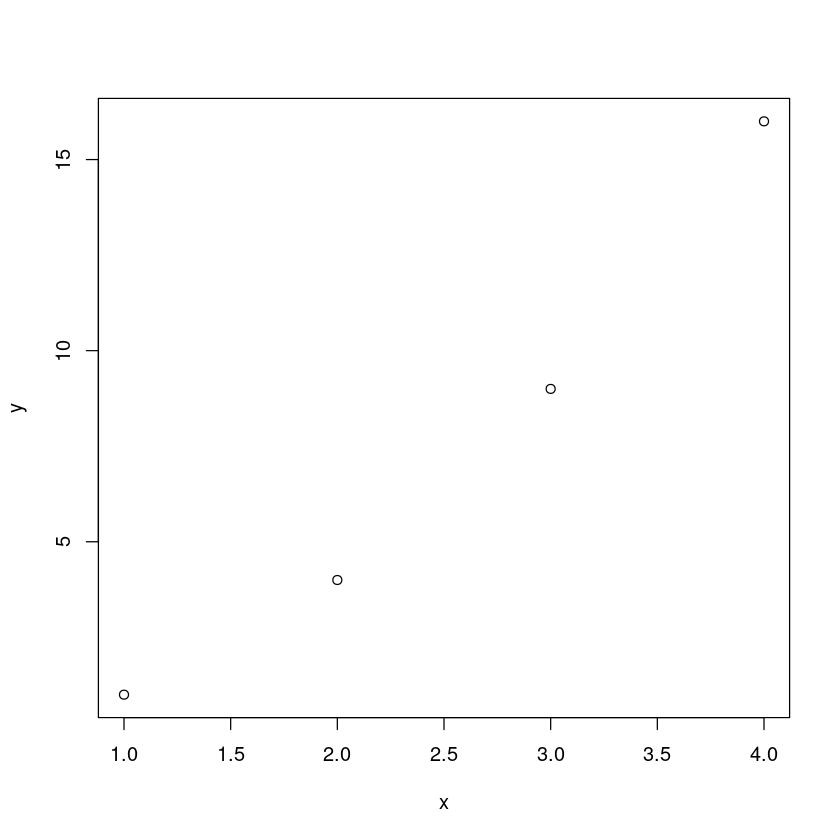
x = c(1, 2, 3, 4)
y = c(1, 4, 9, 16)
plot(x,y)

Quelques autres exemples. Il est aussi possible de personnaliser le style des graphiques de manière très complète.

# vecteurs de points equidistants
t = seq(0., 1, 0.05)
ft <- sin(2* pi *t)
# une droite
plot(t, t, type = "l", xlim = c(0,1), xlab = "Some value", main = "")
# à laquelle on ajoute des points
points(t,t, pch = 19, col = "red")
# on joute une droite en traits tillés du sinus
lines(t, ft, lty = 2)
# the function legend adds a legend
legend("topleft", legend = c("A nice line", "some points"), lty = c(1,NA), pch = c(NA, 19), col = c("black", "red"))
# l'argument lty correspond au type de ligne : la première est une ligne continue, correspondant à la valeur 1
# le second n'est pas une ligne (c'est un point), donc nous fixons la seconde valeur à NA
# l'argument pch correspond au type de point : le premier n'est pas un point mais une ligne, donc on met la deuxième valeur à NA.
# le second est un point correspondant au type de point 19, tel que défini dans la fonction points ci-dessus. 

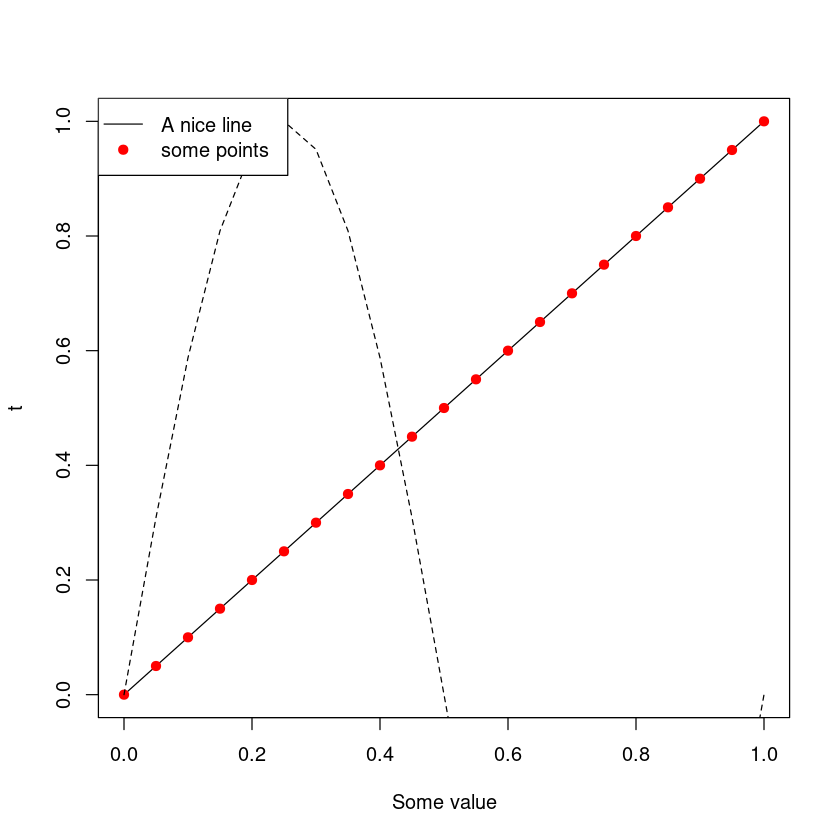
On voit sur le graphique précédent que puisque l’affiche se fait de manière séquentielle puisque d’abord on créé le graphique puis on y ajoute la courbe du sinus, l’échelle est celle fixée automatiquement lors de la création du graphique par la commande plot. Pour pouvoir afficher le sinus, il faut anticiper les limites du graphique avant de créer le graphique. Cela peut se faire à l’aide de la fonction range.

# evenly sampled time at 200ms intervals
t = seq(0., 1, length = 100)
# on créé un vecteur de translations
shift_seq <- seq(0,2 * pi, length.out = 7)
# on déclare une matrice de NA en spécifiant ses composantes
shifted_sine <- matrix(NA, nr = length(t), nc = length(shift_seq)) 
for(i in seq_along(shift_seq))
{
    shifted_sine[,i] <- sin(2* pi *t + shift_seq[i]) # on pose que la ieme colonne est ce vecteur
}
limits_y <- range(c(shifted_sine, t)) # on concatène les valeurs a grapher et on en prend le min et le max
plot(t, t, type = "l", xlim = c(0,1), xlab = "Some value", ylim = limits_y, main = "A nice title")
points(t[seq(1, length(t), 5)],t[seq(1, length(t), 5)], pch = 19, col = "red")
for(i in seq_along(shift_seq))
{
    lines(t, shifted_sine[,i], lty = i, col = i)
}
legend("topleft", legend = c(rep("A nice line", length = length(shift_seq)), "some points"),
       lty = c(seq_along(shift_seq),NA), pch = c(rep(NA, length = length(shift_seq)), 19),
       col = c(seq_along(shift_seq), "red"),bg="transparent")

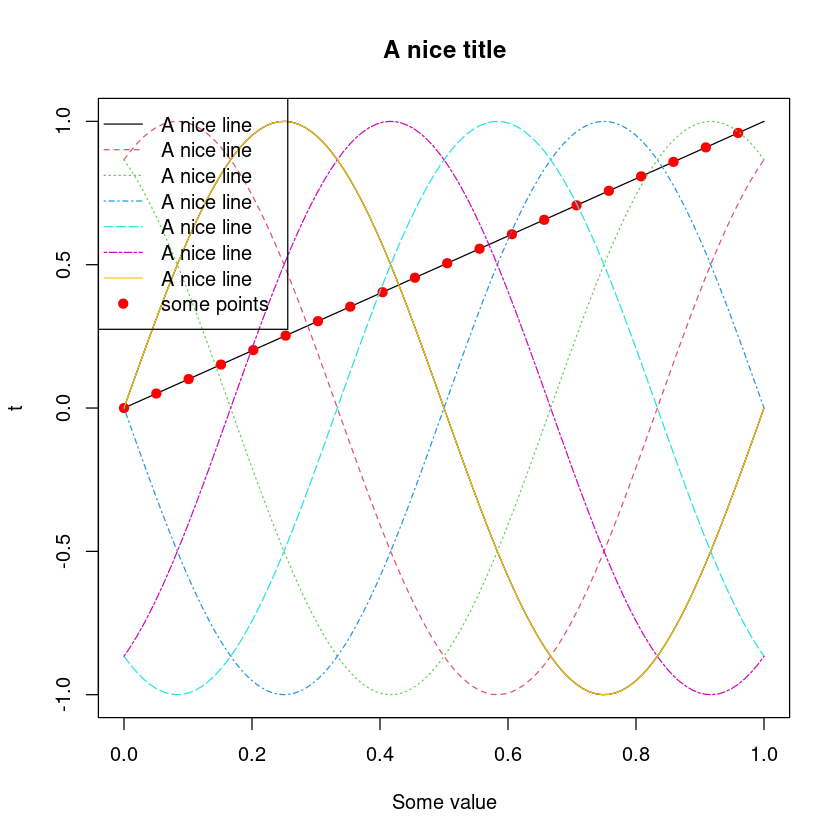
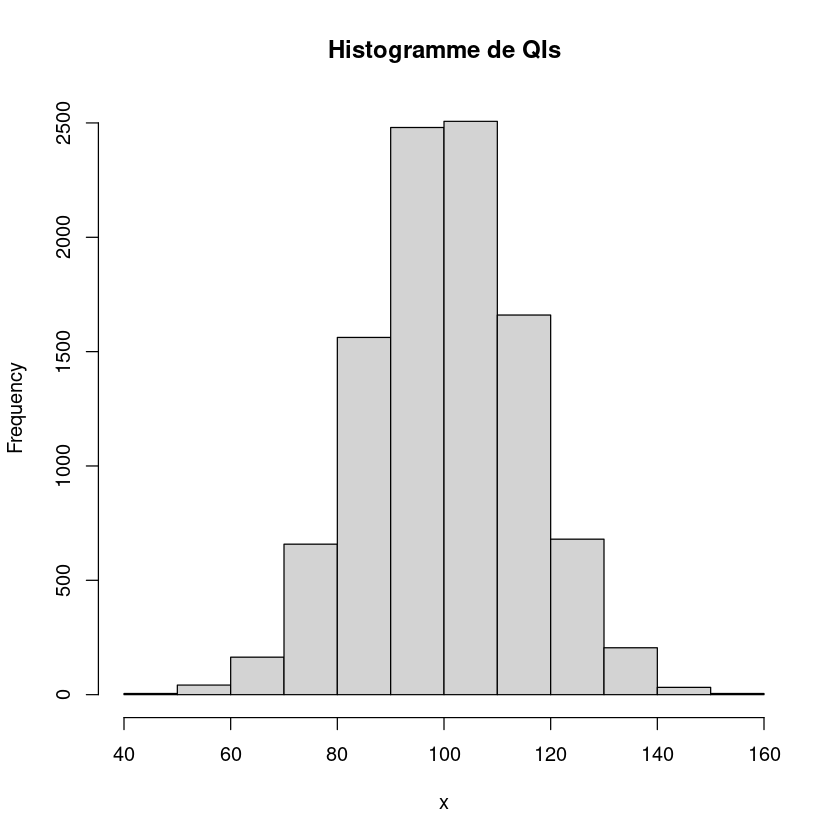
Un exemple d’histogramme:

mu = 100; sigma = 15
x = mu + sigma * rnorm(10000)

# the histogram of the data
hist(x, main = "Histogramme de QIs")

Recherches sur les librairies avec help#

Vous pouvez directement rechercher des informations sur les fonctions des packages installés (mais pas nécessairement chargés). Cela se fait via la commande ? ou help. Par ailleurs, il est possible d’utiliser la commande ?? pour rechercher dans l’aide certains mot-clés.

help(plot)

plot.default {graphics}

R Documentation

The Default Scatterplot Function

Description

Draw a scatter plot with decorations such as axes and titles in the active graphics window.

Usage

## Default S3 method:
plot(x, y = NULL, type = "p",  xlim = NULL, ylim = NULL,
     log = "", main = NULL, sub = NULL, xlab = NULL, ylab = NULL,
     ann = par("ann"), axes = TRUE, frame.plot = axes,
     panel.first = NULL, panel.last = NULL, asp = NA,
     xgap.axis = NA, ygap.axis = NA,
     ...)

Arguments

`x, y`	the `x` and `y` arguments provide the x and y coordinates for the plot. Any reasonable way of defining the coordinates is acceptable. See the function `xy.coords` for details. If supplied separately, they must be of the same length.
`type`	1-character string giving the type of plot desired. The following values are possible, for details, see `plot`: `"p"` for points, `"l"` for lines, `"b"` for both points and lines, `"c"` for empty points joined by lines, `"o"` for overplotted points and lines, `"s"` and `"S"` for stair steps and `"h"` for histogram-like vertical lines. Finally, `"n"` does not produce any points or lines.
`xlim`	the x limits (x1, x2) of the plot. Note that `x1 > x2` is allowed and leads to a ‘reversed axis’. The default value, `NULL`, indicates that the range of the finite values to be plotted should be used.
`ylim`	the y limits of the plot.
`log`	a character string which contains `"x"` if the x axis is to be logarithmic, `"y"` if the y axis is to be logarithmic and `"xy"` or `"yx"` if both axes are to be logarithmic.
`main`	a main title for the plot, see also `title`.
`sub`	a subtitle for the plot.
`xlab`	a label for the x axis, defaults to a description of `x`.
`ylab`	a label for the y axis, defaults to a description of `y`.
`ann`	a logical value indicating whether the default annotation (title and x and y axis labels) should appear on the plot.
`axes`	a logical value indicating whether both axes should be drawn on the plot. Use graphical parameter `"xaxt"` or `"yaxt"` to suppress just one of the axes.
`frame.plot`	a logical indicating whether a box should be drawn around the plot.
`panel.first`	an ‘expression’ to be evaluated after the plot axes are set up but before any plotting takes place. This can be useful for drawing background grids or scatterplot smooths. Note that this works by lazy evaluation: passing this argument from other `plot` methods may well not work since it may be evaluated too early.
`panel.last`	an expression to be evaluated after plotting has taken place but before the axes, title and box are added. See the comments about `panel.first`.
`asp`	the `y/x` aspect ratio, see `plot.window`.
`xgap.axis, ygap.axis`	the `x/y` axis gap factors, passed as `gap.axis` to the two `axis()` calls (when `axes` is true, as per default).
`...`	other graphical parameters (see `par` and section ‘Details’ below).

Details

Commonly used graphical parameters are:

col: The colors for lines and points. Multiple colors can be specified so that each point can be given its own color. If there are fewer colors than points they are recycled in the standard fashion. Lines will all be plotted in the first colour specified.
bg: a vector of background colors for open plot symbols, see points. Note: this is not the same setting as par("bg").
pch: a vector of plotting characters or symbols: see points.
cex: a numerical vector giving the amount by which plotting characters and symbols should be scaled relative to the default. This works as a multiple of par("cex"). NULL and NA are equivalent to 1.0. Note that this does not affect annotation: see below.
lty: a vector of line types, see par.
cex.main, col.lab, font.sub, etc: settings for main- and sub-title and axis annotation, see title and par.
lwd: a vector of line widths, see par.

Note

The presence of panel.first and panel.last is a historical anomaly: default plots do not have ‘panels’, unlike e.g. pairs plots. For more control, use lower-level plotting functions: plot.default calls in turn some of plot.new, plot.window, plot.xy, axis, box and title, and plots can be built up by calling these individually, or by calling plot(type = "n") and adding further elements.

The plot generic was moved from the graphics package to the base package in R 4.0.0. It is currently re-exported from the graphics namespace to allow packages importing it from there to continue working, but this may change in future versions of R.

References

Becker, R. A., Chambers, J. M. and Wilks, A. R. (1988) The New S Language. Wadsworth & Brooks/Cole.

Cleveland, W. S. (1985) The Elements of Graphing Data. Monterey, CA: Wadsworth.

Murrell, P. (2005) R Graphics. Chapman & Hall/CRC Press.

Examples

Speed <- cars$speed
Distance <- cars$dist
plot(Speed, Distance, panel.first = grid(8, 8),
     pch = 0, cex = 1.2, col = "blue")
plot(Speed, Distance,
     panel.first = lines(stats::lowess(Speed, Distance), lty = "dashed"),
     pch = 0, cex = 1.2, col = "blue")

## Show the different plot types
x <- 0:12
y <- sin(pi/5 * x)
op <- par(mfrow = c(3,3), mar = .1+ c(2,2,3,1))
for (tp in c("p","l","b",  "c","o","h",  "s","S","n")) {
   plot(y ~ x, type = tp, main = paste0("plot(*, type = \"", tp, "\")"))
   if(tp == "S") {
      lines(x, y, type = "s", col = "red", lty = 2)
      mtext("lines(*, type = \"s\", ...)", col = "red", cex = 0.8)
   }
}
par(op)

##--- Log-Log Plot  with  custom axes
lx <- seq(1, 5, length.out = 41)
yl <- expression(e^{-frac(1,2) * {log[10](x)}^2})
y <- exp(-.5*lx^2)
op <- par(mfrow = c(2,1), mar = par("mar")-c(1,0,2,0), mgp = c(2, .7, 0))
plot(10^lx, y, log = "xy", type = "l", col = "purple",
     main = "Log-Log plot", ylab = yl, xlab = "x")
plot(10^lx, y, log = "xy", type = "o", pch = ".", col = "forestgreen",
     main = "Log-Log plot with custom axes", ylab = yl, xlab = "x",
     axes = FALSE, frame.plot = TRUE)
my.at <- 10^(1:5)
axis(1, at = my.at, labels = formatC(my.at, format = "fg"))
e.y <- -5:-1 ; at.y <- 10^e.y
axis(2, at = at.y, col.axis = "red", las = 1,
     labels = as.expression(lapply(e.y, function(E) bquote(10^.(E)))))
par(op)

[Package graphics version 4.2.2 ]

?? histogram

R Information

Demos with name or title matching ‘histogram’ using fuzzy matching:


plotly::crosstalk-highlight-binned-target-c
                        Dynamically re-rendering a histogram based on
                        selection


Type 'demo(PKG::FOO)' to run demonstration 'PKG::FOO'.



Help files with alias or concept or title matching ‘histogram’ using
fuzzy matching:


deSolve::plot.deSolve   Plot, Image and Histogram Method for deSolve
                        Objects
DiagrammeR::get_degree_histogram
                        Get histogram data for a graph's degree
                        frequency
  Aliases: get_degree_histogram
flowViz::densityplot    One-dimensional density/histogram plots for
                        flow data
  Aliases: histogram,formula,flowSet-method,
    histogram,formula,flowFrame-method,
    histogram,formula,ncdfFlowSet-method,
    histogram,formula,ncdfFlowList-method
geneplotter::histStack
                        Stacked histogram
ggforce::geom_autodensity
                        A distribution geoms that fills the panel and
                        works with discrete and continuous data
  Aliases: geom_autohistogram
ggplot2::geom_freqpoly
                        Histograms and frequency polygons
  Aliases: geom_histogram
ggpubr::gghistogram     Histogram plot
  Aliases: gghistogram
ggpubr::ggscatterhist   Scatter Plot with Marginal Histograms
ggridges::stat_binline
                        Stat for histogram ridgeline plots
ggstatsplot::gghistostats
                        Histogram for distribution of a numeric
                        variable
ggstatsplot::grouped_ggdotplotstats
                        Grouped histograms for distribution of a
                        labeled numeric variable
ggstatsplot::grouped_gghistostats
                        Grouped histograms for distribution of a
                        numeric variable
gplots::hist2d          Compute and Plot a 2-Dimensional Histogram
graphics::hist          Histograms
graphics::hist.POSIXt   Histogram of a Date or Date-Time Object
graphics::plot.histogram
                        Plot Histograms
  Aliases: plot.histogram, lines.histogram
grDevices::nclass.Sturges
                        Compute the Number of Classes for a Histogram
Hmisc::hist.data.frame
                        Histograms for Variables in a Data Frame
Hmisc::histbackback     Back to Back Histograms
Hmisc::histboxp         Use plotly to Draw Stratified Spike Histogram
                        and Box Plot Statistics
Hmisc::scat1d           One-Dimensional Scatter Diagram, Spike
                        Histogram, or Density
infer::shade_p_value    Shade histogram area beyond an observed
                        statistic
KernSmooth::dpih        Select a Histogram Bin Width
ks::histde              Histogram density estimate
ks::plot.histde         Plot for histogram density estimate
lattice::histogram      Histograms and Kernel Density Plots
  Aliases: histogram, histogram.factor, histogram.numeric,
    histogram.formula
lattice::panel.histogram
                        Default Panel Function for histogram
  Aliases: panel.histogram
lattice::prepanel.default.bwplot
                        Default Prepanel Functions
  Aliases: prepanel.default.histogram
MASS::hist.scott        Plot a Histogram with Automatic Bin Width
                        Selection
MASS::ldahist           Histograms or Density Plots of Multiple Groups
MASS::truehist          Plot a Histogram
mc2d::hist.mc           Histogram of a Monte Carlo Simulation
plot3D::persp3D         Perspective plots, 3-D ribbons and 3-D
                        histograms.
plotly::add_trace       Add trace(s) to a plotly visualization
  Aliases: add_histogram, add_histogram2d, add_histogram2dcontour
pracma::histc           Histogram Count (Matlab style)
pracma::histss          Histogram Bin-width Optimization
psych::multi.hist       Multiple histograms with density and normal
                        fits on one page
psych::pairs.panels     SPLOM, histograms and correlations for a data
                        matrix
psych::scatter.hist     Draw a scatter plot with associated X and Y
                        histograms, densities and correlation
spatstat.explore::kaplan.meier
                        Kaplan-Meier Estimator using Histogram Data
spatstat.explore::km.rs
                        Kaplan-Meier and Reduced Sample Estimator using
                        Histograms
spatstat.explore::panel.contour
                        Panel Plots using Colour Image or Contour Lines
  Aliases: panel.histogram
spatstat.explore::reduced.sample
                        Reduced Sample Estimator using Histogram Data
spatstat.explore::rose
                        Rose Diagram
  Aliases: rose.histogram
spatstat.geom::hist.funxy
                        Histogram of Values of a Spatial Function
spatstat.geom::hist.im
                        Histogram of Pixel Values in an Image
spatstat.geom::transformquantiles
                        Transform the Quantiles
  Concepts: Histogram equalisation
spatstat.geom::whist    Weighted Histogram


Type '?PKG::FOO' to inspect entries 'PKG::FOO', or 'TYPE?PKG::FOO' for
entries like 'PKG::FOO-TYPE'.

Probabilité et statistique (MATH-234(d))

Tutoriel R

Contents