SérieBeta : Correction#

Exercice 1: Biais#

import numpy
import matplotlib.pyplot
import pandas
import scipy.stats

Soit \(X_1, \ldots, X_n\) un échantillon de taille \(n\) de réalisations indépendantes issues d’une distribution de Bernoulli avec paramètre \(p\).

On propose l’estimateur suivant \(\widehat{p}_n\) pour \(p\):

\[\begin{gather*} \widehat{p}_n = \frac{1 + \sum_{i=1}^n X_i}{2 + n} \end{gather*}\]

Question: Quel est le biais de l’estimateur lorsque \(n \to \infty\) ? Écrivez la valeur numérique (approximative à l’ordre \(10^{-2}\)) dans la variable biais.

Solution analytique: On peut calculer le biais par la formule

\[\begin{gather*} \operatorname{biais}(\widehat{p}_n) = \mathbb{E}\left[\widehat{p}_n - p\right] \end{gather*}\]

pour laquelle on trouve, via la linéarité de l’espérance,

\[\begin{align*} \mathbb{E}\left[\widehat{p}_n\right] &= \frac{1}{2+n} \left(1 + \sum_{i=1}^n \mathbb{E}[X_i]\right) \\ &= \frac{1}{2+n} \left(1 + np\right) \\ &= \frac{1}{2+n} + \frac{n}{2+n} p \end{align*}\]

Puisque l’expression ci-dessus tend vers \(p\) lorsque \(n \to \infty\), le biais aussi tend vers \(0\) lorsque \(n \to \infty\).

Note: L’estimateur proposé est utilisé pour éviter une estimation de \(\widehat{p} = 0\) ou \(1\) exactement, ce qui arrive lorsqu’on utilise l’estimateur du maximum de vraisemblance. Voir aussi le lissage de Laplace (https://en.wikipedia.org/wiki/Rule_of_succession).

########### Solution Python: ##########


# Solution numérique par simulation:
# On va approximer le biais par une moyenne de p_n - p sur beaucoup de tirages
n_tirages = 100
n = 1000 # Longueur d'un tirage (doit être grand)
# Puisqu'on ne connait pas p, on va calculer le biais pour plusieurs valeurs possibles de p
valeurs_p = numpy.linspace(start = 0, stop = 1, num = 10)

biais = numpy.zeros(10)
for i in range(0, 10):
    p = valeurs_p[i]
    estim = numpy.zeros(n_tirages)
    for j in range(0, n_tirages):
        tirages = scipy.stats.bernoulli.rvs(p = p, size = n) # Un tirage
        estim[j] = (1 + numpy.sum(tirages)) / (2 + n) # On calcule l'estimateur
    biais[i] = numpy.mean(estim - p) # Le biais pour cette valeur de p

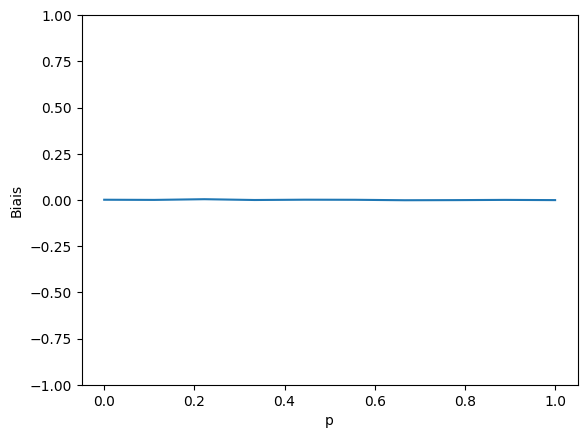
matplotlib.pyplot.plot(valeurs_p, biais)
matplotlib.pyplot.ylabel("Biais")
matplotlib.pyplot.xlabel("p")
matplotlib.pyplot.ylim(-1, 1)
matplotlib.pyplot.show()

# On remarque que le biais est très proche de 0
../../../_images/SolBetaP_6_0.png

Exercice 2: Temps de déboguage#

Une erreur se tapit dans le code de votre projet de bachelor. Chaque membre \(i\) de votre équipe de trois étudiants (\(i \in \{1, 2, 3\}\)) a besoin de \(T_i\) heures pour trouver le bug. On suppose que les temps \(T_i\) ont des distributions exponentielles avec paramètres \(\lambda_1 = 0.1\), \(\lambda_2 = 0.35\), \(\lambda_3 = 0.06\) respectivement.

Un seul membre de votre équipe est choisi au hasard avec probabilités égales pour trouver le bug.

Question: Dans cette situation, avec quelle probabilité est-ce que le bug sera trouvé en moins de 12h? Stockez la valeur dans la variable p.

Solution analytique: Soit \(A = \left\{ \text{le bug est trouvé en moins de 12h }\right\}\). On décompose cet événement selon le choix \(C \in \left\{1,2,3\right\}\) du membre de l’équipe:

\[\begin{align*} P(A) &= \sum_{i=1}^3 P(A \mid C = i) P(C = i) \\ &= \frac{1}{3} \sum_{i=1}^3 P(T_i \leqslant 12) \\ &= \frac{1}{3} \left( 1 - e^{-0.1 \times 12} + 1 - e^{-0.35 \times 12} + 1 - e^{-0.06 \times 12} \right) \\ &\approx \frac{1}{3} (3 - 0.803) \approx 0.732 \end{align*}\]
########### Solution Python: ##########


# On répete sur de nombreux tirages
n = 10000
resultat = numpy.zeros(n) # 1 = Trouvé, 0 = Non
for i in range(0, n):
    T1 = scipy.stats.expon.rvs(scale = 1/0.1, size = 1)
    T2 = scipy.stats.expon.rvs(scale = 1/0.35, size = 1)
    T3 = scipy.stats.expon.rvs(scale = 1/0.06, size = 1)
    Ts = numpy.array([T1, T2, T3]).flatten() # Ce sont les temps qui auraient été pris par tous les membres
    choisi = numpy.random.choice(Ts) # On en choisit un avec probabilités égales
    resultat[i] = 1 * (choisi < 12) # Est ce que le temps était inférieur à 12h ?

p = numpy.mean(resultat)

Exercice 3: Expérience répétée#

Un chercheur souhaite à tout prix démontrer par une expérience un phénomène dont il est convaincu de l’existence. Si le phénomène existe, on suppose que l’expérience le fait apparaitre avec probabilité \(0 < p < 1\). En revanche, si le phénomène n’existe pas, alors l’expérience le fait faussement apparaitre (faux positif) avec probabilité \(0 < q < 1\).

Question: Le chercheur manque de scrupule et répète indépendamment l’expérience jusqu’au premier résultat positif (confirmant l’existence du phénomène). Si \(p = 0.9\), \(q = 0.05\), et si le phénomène existe réelement avec probabilité 50%, donnez la probabilité (dans la variable p) qu’il y arrive en 20 expériences ou moins.

Ensuite, on regarde le nombre \(N\) d’expériences identiques et indépendantes jusqu’au premier succès, ce qui implique que \(N\) a une distribution Géométrique avec paramètre \(p\) ou \(q\) dépendant de l’existence réele du phénomène. Sinon, on peut regarder l’évenement inverse, c’est à dire \(B = \left\{ \text{Aucun succès parmi les 20 premières expériences} \right\} = \left\{ N > 20 \right\}\). En tout cas, on obtient

\[\begin{align*} P(N \leqslant 20 \mid \text{existe}) &= 1 - P(B\mid \text{existe}) = 1 - (1-0.9)^{20}\\ P(N \leqslant 20 \mid \text{n'existe pas}) &= 1 - P(B \mid \text{n'existe pas}) = 1 - (1-0.05)^{20} \end{align*}\]

Enfin, on prend en compte les deux possibilités pour l’existence:

\[\begin{gather*} P(N \leqslant 20) = P(N \leqslant 20 \mid \text{existe}) \times 0.5 + P(N \leqslant 20 \mid \text{n'existe pas}) \times 0.5 \approx 0.5 + 0.64 \times 0.5 \approx 0.82 \end{gather*}\]
########### Solution Python: ##########


# On va répeter l'entièreté du processus un grand nombre de fois
n = 10000
existence = scipy.stats.bernoulli.rvs(p = 0.5, size = n)
au_moins_un_positif = numpy.zeros(n)
for i in range(0, n):
    if existence[i] == 1:
        p = 0.9
    else:
        p = 0.05
    resultats_experiences = scipy.stats.bernoulli.rvs(p = p, size = 20)
    if any(resultats_experiences == 1):
        au_moins_un_positif[i] = 1
    else:
        au_moins_un_positif[i] = 0

p = numpy.mean(au_moins_un_positif)

Exercice 4: Transformation de V.A.#

Soit \(X\sim\mathcal{U}([1,2])\) une variable aléatoire uniforme sur l’intervalle \([1, 2]\) et soit \(Y\) la variable aléatoire donnée par \(Y = \frac{1}{X}\).

Question: Quelle est l’espérance de \(Y\) ? Donnez une valeur approximée à au moins deux décimales dans la variable ey

Solution Analytique: On utilise un changement de variables pour trouver la densité de \(Y\). D’abord, remarquons que \(P(Y < 1/2) = P(1/X < 1/2) = P(X > 2) = 0\), et pareil pour \(P(Y > 1)\). Donc \(Y\) prend presque surement des valeurs dans l’intervalle \([1/2, 1]\). On note aussi que \(Y\) est une variable aléatoire continue.

Pour trouver la densité de \(Y\), on calcule d’abord pour \(1/2 < y < 1\)

\[\begin{gather*} P\left(Y \leqslant y\right) = P\left(\frac{1}{X} \leqslant y\right) = P(X \geqslant 1/y) = 1 - P(X \leqslant 1/y) = 1 - \frac{1/y - 1}{2 - 1} = 2 - 1/y =: F_Y(y) \end{gather*}\]

Suivant quoi la densité se trouve par

\[\begin{gather*} f_Y(y) = \frac{\partial F_Y(y)}{\partial y} = 1/y^2 \end{gather*}\]

pour \(1/2 < y < 1\).

Pour calculer l’espérance, on intègre:

\[\begin{gather*} \mathbb{E}\left[Y\right] = \int_{1/2}^1 y f_Y(y) \, dy = \int_{1/2}^1 1/y \, dy = \log 1 + \log 2 = \log 2 \end{gather*}\]
########### Solution Python: ##########

n = 100000
x = scipy.stats.uniform.rvs(loc = 1, scale = 1, size = n)
y = 1/x
ey = numpy.mean(y)

Exercice 5: Estimateur du maximum de vraisemblance#

On observe un échantillon \(x_1,\dots, x_n\) de réalisations indépendantes d’une loi de Poisson de paramètre \(\lambda\), dont les valeurs sont rapportées ci-dessous:

Valeurs

\(x_1\)

\(x_2\)

\(x_3\)

\(x_4\)

\(x_5\)

\(x_6\)

\(x_7\)

\(x_8\)

\(x_9\)

1

0

2

1

3

0

1

2

1

  1. Calculez l’estimateur du maximum de vraisemblance de \(\lambda\) que vous stockerez dans la variable estim.

La fonction de vraisemblance est, à une constante près,

\[\begin{gather*} \ell(\lambda) = \sum_{i=1}^n x_i \log \lambda - n\lambda \end{gather*}\]

pour lequel le maximum est \(\widehat{\lambda} = \frac{1}{n} \sum_{i=1}^n x_i\).

valeurs = numpy.array([1, 0, 2, 1, 3, 0, 1, 2, 1])
estim = numpy.mean(valeurs)

  1. Calculer un intervalle de confiance approximatif à 95% pour ce paramètre, basé sur la distribution asymptotique du l’estimateur du maximum de vraisemblance et stockez-le dans le vecteur ci à deux composantes ci-dessous en y remplaçant les valeurs manquantes (numpy.nan ou NA) par votre réponse.

Solution:

On trouve pour l’information de Fisher théorique

\[\begin{gather*} I(\lambda) = -\mathbb{E}\left[\frac{\partial^2}{\partial \lambda^2} \ell(\lambda)\right] = n/\lambda \end{gather*}\]

L’information observée est de

\[\begin{gather*} \widehat{I}_n = n/\widehat{\lambda} = \frac{n^2}{\sum_{i=1}^n x_i} = 9^2 / 11 \end{gather*}\]

Et donc la variance asymptotique de l’estimateur est de

\[\begin{gather*} \widehat{I}_n^{-1} = 11/81 \approx 0.1358 \end{gather*}\]

L’intervalle de confiance demandé est donc

\[\begin{gather*} \widehat{\lambda} \pm z_{1-\alpha/2} \sqrt{0.1358} \approx [0.499, 1.944] \end{gather*}\]
ci = estim + numpy.array([-1.96, 1.96]) * numpy.sqrt(estim/len(valeurs))

Exercice 6: Statistiques descriptives#

On considère le jeu de données ci-dessous décrivant la taille, le poids et la couleur du poil de 5 races de chien domestique (identifiés par id).

chiens = pandas.DataFrame.from_dict({
    'id' : [1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5],
    'poids' : [9.69, 9.87, 9.9, 8.43, 8.8, 9.64, 4.92, 7.13, 5.12, 11.82, 10.32, 10.64, 11.94, 11.51, 11.17],
    'taille' : [1.02, 0.68, 0.74, 0.8, 0.48, 0.44, 0.5, 0.44, 0.7, 1.66, 0.52, 1.46, 0.68, 0.84, 0.74],
    'poil' : ["noir", "clair", "brun", "clair", 
"noir", "brun", "noir", "clair", "brun", "brun", "clair", "noir", 
"noir", "clair", "brun"]})
print(chiens)

    id  poids  taille   poil
0    1   9.69    1.02   noir
1    1   9.87    0.68  clair
2    1   9.90    0.74   brun
3    2   8.43    0.80  clair
4    2   8.80    0.48   noir
5    2   9.64    0.44   brun
6    3   4.92    0.50   noir
7    3   7.13    0.44  clair
8    3   5.12    0.70   brun
9    4  11.82    1.66   brun
10   4  10.32    0.52  clair
11   4  10.64    1.46   noir
12   5  11.94    0.68   noir
13   5  11.51    0.84  clair
14   5  11.17    0.74   brun

  1. Calculez la moyenne empirique et la variance empirique (les deux versions de la variance sont acceptées ici, à la différence du point suivant) des colonnes poids et taille.

moy_poids = numpy.mean(chiens["poids"])
var_poids = numpy.var(chiens["poids"], ddof = 1)

  1. On suppose que les tailles sont issues d’une seule distribution normale \(N(\mu, \sigma^2)\) pour tous les chiens. Construisez un intervalle de confiance à 95% pour le paramètre \(\mu\) de cette distribution dans la variable ci (Attention: utilisez un estimateur non-biaisé de \(\sigma^2\)).

Solution: L’intervalle est celui basé sur la distribution \(t\) avec \(n - 1\) degrés de liberté, c’est-à-dire

\[\begin{gather*} \widehat{\mu} \pm t_{1-\alpha/2, n-1} \frac{\widehat{\sigma}}{\sqrt{n}} \end{gather*}\]
########### Solution Python: ##########

n = numpy.size(chiens, 0)
ci = moy_poids + scipy.stats.t.ppf([0.025, 0.975], df = n - 1) * numpy.sqrt(var_poids) / numpy.sqrt(n)