8. Valeurs caractéristiques

\[\newcommand\E{\mathbb{E}} \newcommand\var{\text{Var}} \newcommand\cov{\text{Cov}} \newcommand\corr{\text{Corr}}\]

Une variable aléatoire est caractérisée par sa fonction de masse ou sa densité \( f_X \) mais cette dernière ne donne pas beaucoup d’intuition sur \( X \). Quelques valeurs caractéristiques donnent une meilleure intuition. On va en particulier voir les notions suivantes :

• Espérance, espérance conditionnelle et loi de l’espérance totale.

• Variance.

• Covariance, corrélation.

• Standardisation d’une variable aléatoire.

8.1. Mesure de tendance centrale

Définition 8.1 (Espérance)

L’espérence d’une variable aléatoire \(X\) est:

\[\begin{gather*} \E[X] = \left\{ \renewcommand{\arraystretch}{1.5} \begin{array}{ll} \displaystyle\sum_i x_i f_X (x_i) & \text{si X est discrète,} \\ \displaystyle \int_{-\infty}^{\infty} x\ f_X (x) dx & \text{si X est continue.} \end{array} \right. \end{gather*}\]

Interprétation de l’espérance

• interprétation 1: centre de gravité d’un ensemble de masses;

• interprétation 2: moyenne pondérée par des masses.

Propriété 8.1 (Espérance)

L’espérance est linéaire. En d’autres termes, cela signifie que:

• pour toutes constantes \(a,b \in \mathbb{R}\), et pour toute variable aléatoire \(X\), on a

\[\begin{gather*} \E[ a X + b] = a \E[X] + b; \end{gather*}\]

• pour toutes variables aléatoires \(X_1, \dots, X_n\), l’espérance d’une somme est la somme des espérances

\[\begin{gather*} \E\left[ \sum_{i=1}^n X_i \right] = \sum_{i=1}^n \E[X_i].\end{gather*}\]

• Notez en particulier pour tout \(a \in \mathbb{R},\) on a bien \(\E[a] = a\).

• Si \(X\) et \(Y\) sont indépendantes, alors \(\E[XY] = \E[X] \E[Y].\)

Proposition 8.1 (Espérance d’une fonction de \(X\))

L’espérance peut aussi être appliquée à des variables définies comme fonctions de \(X\): Pour toute fonction (raisonnable) \(g\), on a :

\[\begin{gather*} \E\left[ g(X) \right] = \left\{ \renewcommand{\arraystretch}{1.5} \begin{array}{ll} \displaystyle \sum_i g(x_i) f_X (x_i) & \text{si X est discrète,} \\ \displaystyle \int_{-\infty}^{\infty} g(x) f_X (x) dx & \text{si X est continue.} \end{array} \right. \end{gather*}\]

Proposition 8.2 (Caractérisation de l’indépendance par l’espérance)

\(X,Y\) sont indépendantes si et seulement si pour toute fonctions \(g,h\), on a:

\[\begin{gather*} \E\left[ g(X) h(Y) \right] = \E\left[ g(X) \right] \E\left[h(Y) \right] . \end{gather*}\]

Propriété 8.2 (Espérance)

Pour tout événement \(A \subset \Omega\), on peut exprimer la probabilité de cet événement à l’aide de l’espérance. En effet, on a:

\[\begin{gather*} \mathbb{P}(A) = \E[\mathbf{1}_{A}(x)], \end{gather*}\]

où \(\mathbf{1}_{A}(x)\) est la fonction indicatrice de l’événement \(A\).

Définition 8.2 (Espérance conditionnelle)

Soient \(X,Y\) deux variables aléatoires. L’espérance conditionnelle d’une variable aléatoire \(X\) sachant \(Y\) est:

\[\begin{gather*} \E[X|Y = y] = \left\{ \renewcommand{\arraystretch}{1.5} \begin{array}{ll} \displaystyle \sum_i x_i f_{X|Y}(x_i, y) & \text{si $X,Y$ sont discrètes,} \\ % = \frac{1}{f_Y(y)}\sum_i x_i f_{X,Y}(x_i, y) \displaystyle \int_{-\infty}^{\infty} x\ f_{X|Y}(x, y) dx & \text{si $X$ est continue,} \end{array} \right. \end{gather*}\]

En fait, l’espérance conditionnelle est une fonction de la variable aléatoire \(Y\); ainsi \(\E[X|Y]\) est une variable aléatoire, dont l’espérance coïncide avec l’espérance de \(X\). Ce résultat peut paraître très obscur et sa portée est difficile à mesurer en un premier temps. Toutefois, l’espérance conditionnelle joue un rôle très important en probabilité et en statistique car elle permet de caractériser les meilleurs prédicteurs.

Théorème 8.1 (Loi de l’espérance totale)

Soient \(X,Y\) deux variables aléatoire d’espérance finie. Alors on a l’égalité suivante:

\[\begin{gather*} \E[ \E[X|Y]] = \E[X]. \end{gather*}\]

Exemple 8.1 (Espérance d’une variable binomiale)

Soit \(X \sim \mathcal{B}(n, p)\), calculer \( \E[X] \).

Solution

On a deux solutions:

• en faisant des calculs brutaux impliquant des coefficients binomiaux;

• en utilisant l’additivité de l’espérance.

En effet, une variable binomiale est une somme de \( n \) variables de Bernoulli indépendantes. Soit \(X\sim \mathcal{B}(n,p)\). Alors on a \(X = \sum_{k = 1}^n I_k,\) où \(I_1, \dots, I_n \stackrel{idd}{\sim} \mathcal{B}(p).\) On a donc:

\[\begin{align*} \E\left[X\right] &= n \sum_{k = 1}^n \underbrace{\E\left[I_k\right]}_{= p} = n p, \\ % \var\left( X \right) &= n p (1-p). \end{align*}\]

Exemple 8.2 (Espérance d’une variable Poisson)

Soit \( X \sim \text{Poiss}(\lambda) \), calculer \( \E[X] \).

Solution

Dans cet exemple, la seule solution est de faire un calcul brutal. Soit \(X\sim Poiss(\lambda)\)

\[\begin{align*} \E\left[X\right] &= \sum_{k=0}^\infty k \cdot \frac{\lambda^k}{k!} e^{-\lambda} = 0 + \sum_{k=1}^\infty \frac{\lambda^{k}}{(k-1)!} e^{-\lambda} \\ &= e^{-\lambda}\lambda \sum_{k = 1}^\infty \frac{\lambda^{k-1}}{(k-1)!} =e^{-\lambda}\lambda \sum_{k = 0}^\infty \frac{\lambda^{k}}{k!} = \lambda. \\ \end{align*}\]

Exemple 8.3 (Moyenne d’une Gaussienne)

Soit \( X \sim \mathcal{N}(\mu, \sigma) \), calculer \( \E[X] \).

Solution

Pour ce dernier exemple, la solution est d’utiliser quelques astuces. Pour la moyenne, on utilise la symétrie de la densité. En effet, pour n’importe toute densité \(f(x)\) et pour tout réel \(\mu \in \mathbb{R}\), on a

\[\begin{gather*}\int_{-\infty}^\infty \mu f(x) \ dx = \mu\int_{-\infty}^\infty f(x) \ dx = \mu.$\end{gather*}\]

\[\begin{align*} \E[X] &= \int_{-\infty}^\infty x \frac{1}{\sigma \sqrt{2\pi}} \exp\left(- \frac{(x-\mu)^2}{2\sigma^2} \right) dx \\ &= \mu + \int_{-\infty}^\infty \frac{x-\mu}{\sigma \sqrt{2\pi}} \exp\left(- \frac{(x-\mu)^2}{2\sigma^2} \right) dx \\ &= \mu + \int_{\mu}^\infty \frac{(x-\mu)}{\sigma \sqrt{2\pi}} \exp\left(- \frac{(x-\mu)^2}{2\sigma^2} \right) dx \\ & - \int_{\mu}^\infty \frac{(x-\mu)}{\sigma \sqrt{2\pi}} \exp\left( -\frac{(x-\mu)^2}{2\sigma^2} \right) dx = \mu + 0 = \mu. \end{align*}\]

8.2. Mesure de dispersion

8.2.1. Variance

Définition 8.3 (Variance)

La variance d’une variable aléatoire \( X \) est définie comme:

\[\begin{gather*} \var(X) = \E\left[ \left(X - \E[X] \right)^2 \right] = \E[X^2] - \E[X]^2 \end{gather*}\]

Propriété 8.3 (Variance)

• \( \var(X) \geq 0 \).

• \( \var(X) = 0 \) si et seulement si \( X \) est constante.

• La déviation standard (écart-type) est: \( \sigma(X) = \sqrt{\var(X)} \geq 0 \)

• \( \var( a X + b ) = a^2 \var(X) \) pour toutes constantes \(a,b \in \mathbb{R}\).

• Si \(X,Y\) sont indépendantes, alors \( \var(X + Y) = \var(X) + \var(Y) \).

Exemple 8.4 (Variance d’une variable de Poisson)

Si \( X \sim \text{Poiss}(\lambda)\), montrer que \( \var(X) = \lambda \) en commençant par calculer \( \E[X(X-1)] \).

Solution

On calcule (astuce!) \( \E[X (X-1) ],\) et on obtient:

\[\begin{align*} \E\left[X (X-1)\right] &= \sum_{k=0}^\infty k (k-1) \cdot \frac{\lambda^k}{k!} e^{-\lambda} = 0 + 0 + \sum_{k=2}^\infty \frac{\lambda^{k}}{(k-2)!} e^{-\lambda} \\ &= e^{-\lambda}\lambda^2 \sum_{k = 2}^\infty \frac{\lambda^{k-2}}{(k-2)!} =e^{-\lambda}\lambda^2 \sum_{k = 0}^\infty \frac{\lambda^{k}}{k!} = \lambda^2. \\ \end{align*}\]

On en déduit:

\[\begin{align*} \E(X^2) &= \E[X (X-1) ] + \E[X] = \lambda^2 + \lambda \\ \var(X) &= \E[X^2] - \E[X]^2 = \lambda. \end{align*}\]

Exemple 8.5 (Variance d’une variable binomiale)

Si \( X \sim \mathcal{B}(n,p) \), montrer que \( \var(X) = n p (1-p) \).

Solution

Tout d’abord, on note que pour \( I \sim \mathcal{B}(p) \), \(I^2 = I\) et donc

\[\begin{gather*}\E[I^2] = \E[I] \Rightarrow \var(I) =\E[I^2] - \left(\E[I]\right)^2 = p -p^2 = p(1-p). \end{gather*}\]

Soit \( X \sim \mathcal{B}(n,p) \). Alors on a \(X = \sum_{k = 1}^n I_k,\) où \(I_1, \dots, I_n \stackrel{idd}{\sim} \mathcal{B}(p).\) Ainsi,

\[\begin{gather*}\var(X) = \var \left(\sum_{k = 1}^n I_k \right) = \sum_{k = 1}^n \underbrace{\var\left(I_k \right)}_{= p(1-p)} = n p(1-p).\end{gather*}\]

Exemple 8.6 (Variance d’une Gaussienne)

Si \( X \sim \mathcal{N}(\mu,\sigma^2) \), montrer que \( \var(X) = \sigma^2 \) à l’aide d’une intégration par parties: \( u(x) = (x - \mu)\) et \( v'(x) = (x-\mu) f(x) \).

Solution

Pour la variance, on fait une intégration par parties:

\[\begin{align*} \var(X) &= \int_{-\infty}^\infty \frac{(x-\mu)^2}{\sigma \sqrt{2\pi}} \exp\left(- \frac{(x-\mu)^2}{2\sigma^2} \right) dx \\ &= \left[ (x-\mu) (-\sigma^2) \frac{1}{\sigma \sqrt{2\pi}} \exp\left(- \frac{(x-\mu)^2}{2\sigma^2} \right) \right]_{-\infty}^\infty \\ & - \int_{-\infty}^\infty (-\sigma^2) \frac{1}{\sigma \sqrt{2\pi}} \exp\left(- \frac{(x-\mu)^2}{2\sigma^2} \right) \\ &= 0 + \sigma^2 \end{align*}\]

Définition 8.4 (Covariance)

La covariance mesure la dépendance linéaire entre \(X\) et \(Y\):

\[\begin{align*} \cov(X,Y)& = \E\left[ \bigg(X - \E[X] \bigg) \bigg(Y - \E[Y] \bigg) \right] \\ &= \E[X Y] - \E[X] \E[Y]. \end{align*}\]

Propriété 8.4 (Covariance)

• \( \cov(X,X) = \var(X) \)

• \( \cov(X,Y) = \cov(Y,X) \)

• \( \cov(X+Y, Z) = \cov(X,Z) + \cov(Y,Z) \)

• \( \cov(a X + b, c Y + d) = ac \, \cov(X,Y) \)

• \( \var(X + Y) = \var(X) + \var(Y) + 2 \cov(X,Y) \)

• Si \(X,Y\) sont indépendantes, \( \cov(X,Y) = 0 \)

Attention

L’inverse n’est pas vrai !!

Exemple 8.7

La densité conjointe de \(X,Y\) est:

\[\begin{gather*} f_{X,Y}(x,y) = \left\{ \begin{array}{cl} x+y & \text{si } 0<x<1, 0<y<1 \\ 0 & \text{sinon} \end{array} \right. \end{gather*}\]

Trouver \( \var(X), \var(Y), \cov(X,Y) \).

Solution

On a déjà calculé précédemment la densité marginale: \( f_X(x) = (x + 1/2) \mathbf{1}_{[0,1]}(x)\). On peut donc calculer la moyenne et variance de \( X \)

\[\begin{align*} \E[X] &= \int_0^1 x (x+1/2)dx = \int_0^1 (x^2 + x/2)dx = \frac{1}{3} + \frac{1}{4} =\frac{7}{12}, \\ \E[X^2] &= \int_0^1 x^2 (x+1/2)dx = \int_0^1 (x^3 + x^2/2)dx = \frac{1}{4} + \frac{1}{6} = \frac{5}{12}, \\ \var(X) &= \frac{60-49}{144} = \frac{11}{144}. \end{align*}\]

Par symétrie, \(Y\) a la même espérance et variance que \(X\).

On trouve la covariance en calculant:

\[\begin{align*} \E[XY] &= \int_0^1 x y (x+y) dx dy \\ &= \int_0^1 \int_0^1 (x^2 y + x y^2) dx dy \\ &= 2 \int_0^1 \int_0^1 x^2 y dx dy \\ &= 2 \cdot 1/2 \int_0^1 x^2 dx \\ &= 1 / 3 \\ \cov(X,Y) &= \E[XY] - \E[X] \E[Y] \\ &= 1/3 - 49/144 \\ &= -1/144 \end{align*}\]

8.2.2. Corrélation

Définition 8.5 (Corrélation)

La corrélation de \(X,Y\) est une mesure de la dépendance linéaire entre \(X\) et \(Y\). C’est une version normalisée de la covariance:

\[\begin{gather*} \corr(X,Y) = \rho(X,Y) = \frac{\cov(X,Y)}{ \sqrt{\var(X) \var(Y) } }. \end{gather*}\]

Propriété 8.5 (Corrélation)

• \( \corr(X,Y) = \corr(Y,X) \);

• \( \corr(X,X) = 1 \);

• \( \corr(X,-X) = -1 \);

• \( -1 \leq \corr(X,Y) \leq 1 \) (inégalité de Cauchy-Schwarz);

• Si \(X,Y\) sont indépendantes, alors \( \corr(X,Y) = 0\) (mais la réciproque est fausse).

Remarque 8.1

\( \cov(.,.) \) est une forme de produit scalaire. Ainsi, beaucoup d’analogies existent. Ainsi

• \(\var(\cdot)\) est une norme;

• le fait que \(\corr(\cdot, \cdot)\in[0,1]\) vient de l’inégalité de Cauchy-Schwarz. En particulier, en reprenant l’analogie vectorielle, on a:

\[\begin{gather*}\corr(X,Y) = \frac{\cov(X,Y)}{\sqrt(\var(X) \var(Y))} = \frac{\langle X,Y\rangle}{\|X\| \|Y\|} = \cos(\theta),\end{gather*}\]

où \(\theta\) désigne « l’angle » entre \(X\) et \(Y\);

• les notions de meilleure approximation (projection) ont aussi des analogies en probabilités.

Fig. 8.1 : Exemples de corrélation. L’exemple en bas à gauche montre qu’il peut exister une relation claire entre \(X,Y\) sans que la corrélation ne la détecte.

Fig. 8.2 : Scatterplot de la valeur prédite en fonction de la valeur observée. \(\rho = 0.707\).

8.2.3. Corélation et causalité

Corrélation n’implique pas la causalité !! (Messerli, 2012 NEJM)

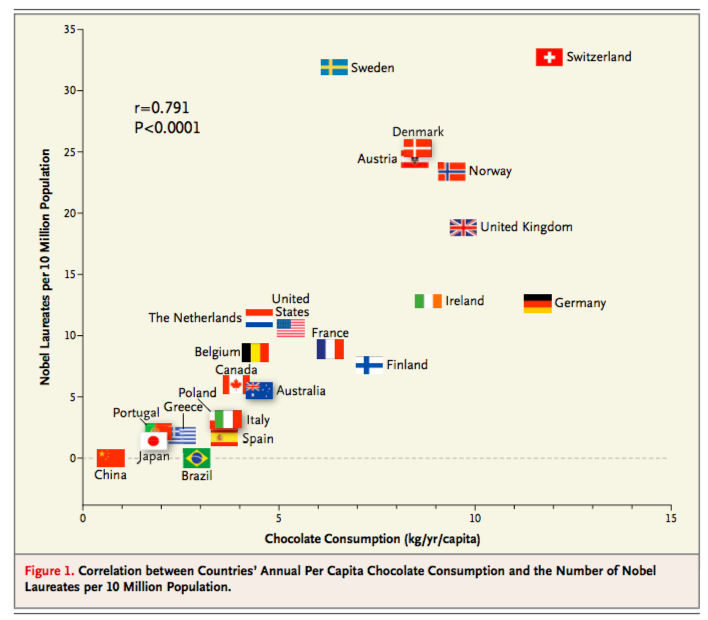
Fig. 8.3 : Nombre de prix Nobel en fonction de la consommation de chocolat.

On a vu des exemples de l’absence de lien entre corrélation et causalité. On peut en tirer deux constats:

• Le premier est que la corrélation ne permet pas de déduire si deux variables sont une fonction déterministe l’une de l’autre.

• Le second est que même si un lien est mis en évidence, celui-ci n’établit pas de relation causale.
  Essayez donc de manger plus de chocolat pour voir si un prix Nobel va vous vous être décérné!

• Si \( A \) cause \( B \): alors \( A, B \) peuvent être corrélées.

• Si \( B \) cause \( A \): alors \( A, B \) peuvent être corrélées.

• Si \( C \) cause \( A \) et \( B \) : alors \( A, B \) peuvent être corrélées.

On ne peut pas distinguer ces trois scénarios juste en observant une corrélation. Seule une expérience active / avec intervention permet de tester la causalité.

La plupart du temps, la présence de corrélation entre \( A \) et \( B \) est due à une cause commune… ou pas. De même, l’absence de corrélation n’indique pas l’absence de lien.

De nombreux travaux (certains très récents) visent à développer des méthodes pour établir (ou rejeter) un lien entre deux variables aléatoires, c’est-à-dire pour tester l’hypothèse d’indépendance.

• (Brownian) Distance correlation: G. Székely and M. Rizzo (2007, 2009);

• A new correlation coefficient: S. Chatterjee (+2021);

• voir Shi, Drton et Han (+2021) pour une discussion plus générale.

Supposons que pour une population finie connue notée \(Y\), on cherche à étudier l’efficacité d’un traitement \(A\).

\[\begin{gather*} Y = \left\{ \begin{array}{cl} 1 & \text{si l'individu est malade} \\ 0 & \text{sinon} \end{array} \right. \ \end{gather*}\]

et

\[\begin{gather*} A = \left\{ \begin{array}{cl} 1 & \text{si l'individu reçoit un traitement} \\ 0 & \text{sinon} \end{array} \right. \end{gather*}\]

Alors \(Y\) et \(A\) sont \textit{associées} si

\[\begin{gather*} \Pr(Y = 1 | A = 1) \neq \Pr(Y = 1 | A = 0). \end{gather*}\]

La question de la causalité peut se résumer par l’interrogation
« Et si ? » Supposons qu’un individu, Bertrand, soit exposé à des produits émis par une usine pétro-chimique aujourd’hui démantelée et voisine de son domicile et développe une maladie grave. Supposons aussi que l’on ait accès à une réalité parallèle où Bertrand aurait exactement la même vie, à la différence près que l’usine n’aurait jamais été construite et que dans cette vie, Bertrand n’aurait pas développé de maladie.
Alors on peut conclure que la présence de l’usine a causé sa maladie grave.

Pour étudier à une relation causale entre deux facteurs (l’usine et le fait d’être malade) et pour un contexte fixé (la vie de Bertrand), on compare alors une situation réellement advenue (présence de l’usine) et une situation hypothétique (absence de l’usine) et l’effet sur la maladie.

La causalité s’exprime alors comme la différence entre la situation réelle et une situation inobservée, que l’on appelle contre-factuelle.

Exemple 8.8

Les dieux de l’Olympe sont tous atteints d’une maladie grave, l’orgueil. Esculape, le médecin de l’équipe, pense avoir trouvé un remède. Pour le tester, il propose à certains dieux de prendre ce traitement, qui devrait faire effet dans les 5 jours.

• On note \(A\) la variable indicatrice de la prise de traitement;

• On note \(Y\) la variable indicatrice de la guérison après 5 jours;

• On note \(Y^{A = a}\) pour signifier la variable indicatrice de guérison après avoir pris ou pas le traitement, i.e. \(a \in \{0,1\}\).

Autrement dit …

Esculape, conscient des limites de son plan d’expérience, décide de demander l’aide de Chronos (à ne pas confondre avec Cronos), qui gère le temps sur l’Olympe. Il revient dans le temps et assigne à chaque dieux l’exact contraire du traitement qu’ils avaient initialement choisi.

On obtient alors le tableau suivant.

Notons la différence:

• \( \Pr(Y = 1| A = 1) = 7/13 \neq \Pr(Y = 1| A = 0) = 3/7\): association;

• \( \Pr(Y^{A = 1} = 1) = 1/2 = \Pr(Y^{A = 0} = 1)\): pas de causalité!